Die Höhe eines Binärbaums in C/C++: Anleitung & Beispiel
Die Höhe eines Binärbaums wird als die maximale Tiefe eines Blattknotens vom Wurzelknoten aus definiert. Das heißt, es ist die Länge des längsten Pfades vom Wurzelknoten zu einem beliebigen Blattknoten.
Beispiel für einen Binärbaum
Betrachten wir den folgenden Binärbaum.
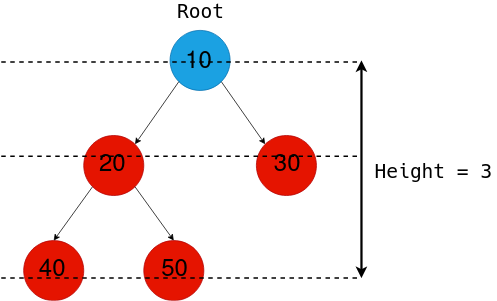Da die Blattknoten, die der maximalen Tiefe entsprechen, 40 und 50 sind, finden wir die Höhe, indem wir die Anzahl der Kanten vom Wurzelknoten zu einem dieser beiden Knoten zählen, was 3 ergibt.
Erstellen eines Algorithmus zur Bestimmung der Höhe eines Binärbaums
Jetzt, da wir wissen, was die Höhe eines Binärbaums bedeutet, werden wir einen Algorithmus entwickeln, um die Höhe eines beliebigen Binärbaums zu bestimmen.
Logik zur Bestimmung der Höhe eines Binärbaums in C/C++
Nun wollen wir die Logik zur Bestimmung der Höhe festlegen und zuerst unseren Pseudocode schreiben.
Wir verwenden Rekursion im Baum, um die Höhe zu bestimmen. (Siehe den Wikipedia-Artikel für die Konzepte)
Da die Höhe des Baums als der größte Pfad von der Wurzel zu einem Blatt definiert ist, können wir die Höhe der linken und rechten Teilbäume rekursiv berechnen.
Wir können die Definition der Höhe jetzt auf die Teilbäume anwenden.
Wir beobachten, dass es das Maximum zwischen dem linken und dem rechten Teilbaum ist, zu dem wir eins addieren.
Da die Höhe des Baums die maximale Höhe des Teilbaums + 1 ist, machen wir so weiter, bis der Teilbaum NULL wird und seine Höhe 0 ist.
An diesem Punkt wird unsere Funktion schließlich beendet, und
Die Funktion tree_height()
Schreiben wir die Funktion tree_height(), die die Höhe berechnet.
// Find height of a tree, defined by the root node
int tree_height(Node* root) {
if (root == NULL)
return 0;
else {
// Find the height of left, right subtrees
left_height = tree_height(root->left);
right_height = tree_height(root->right);
// Find max(subtree_height) + 1 to get the height of the tree
return max(left_height, right_height) + 1;
}
Zeile #3 überprüft die Abbruchbedingung, wenn die Größe des Teilbaums 0 ist oder wenn der Wurzelknoten NULL ist.
Zeilen 7 und 8 finden rekursiv die Höhe der linken und rechten Teilbäume.
Und schließlich gibt Zeile 11 das Maximum der beiden zurück und damit die Höhe eines Binärbaums.
Implementierung in C/C++
Das Folgende ist ein vollständiges Programm, das zeigt, wie der Binärbaum erstellt wird, und dann die Logik zur Bestimmung der Höhe in tree_height() zeigt, also die Höhe eines Binärbaums in C/C++.
#include <stdio.h>
#include <stdlib.h>
typedef struct Node Node;
// Define the Tree Node here
struct Node {
int value;
// Pointers to the left and right children
Node* left, *right;
};
Node* init_tree(int data) {
// Creates the tree and returns the
// root node
Node* root = (Node*) malloc (sizeof(Node));
root->left = root->right = NULL;
root->value = data;
return root;
}
Node* create_node(int data) {
// Creates a new node
Node* node = (Node*) malloc (sizeof(Node));
node->value = data;
node->left = node->right = NULL;
return node;
}
void free_tree(Node* root) {
// Deallocates memory corresponding
// to every node in the tree.
Node* temp = root;
if (!temp)
return;
free_tree(temp->left);
free_tree(temp->right);
if (!temp->left && !temp->right) {
free(temp);
return;
}
}
int tree_height(Node* root) {
// Get the height of the tree
if (!root)
return 0;
else {
// Find the height of both subtrees
// and use the larger one
int left_height = tree_height(root->left);
int right_height = tree_height(root->right);
if (left_height >= right_height)
return left_height + 1;
else
return right_height + 1;
}
}
int main() {
// Program to demonstrate finding the height of a Binary Tree
// Create the root node having a value of 10
Node* root = init_tree(10);
// Insert nodes onto the tree
root->left = create_node(20);
root->right = create_node(30);
root->left->left = create_node(40);
root->left->right = create_node(50);
// Find the height of the tree
int height = tree_height(root);
printf(„Height of the Binary Tree: %d\n“, height);
// Free the tree!
free_tree(root);
return 0;
}
