Deep Learning mit PyTorch: Training, Validierung und Genauigkeit
Einführung
Im Bereich des Deep Learnings bieten die meisten Frameworks keine vorgefertigten Trainings-, Validierungs- und Genauigkeitsfunktionen. Viele Ingenieure finden daher den Einstieg in diese Funktionalitäten schwierig, wenn sie erstmals Datenwissenschaftsprobleme angehen. In den meisten Fällen implementieren Entwickler diese Prozesse manuell, was komplex werden kann. Um diese Funktionen zu schreiben, muss man die Prozesse genau verstehen. Dieses Anfängertutorial erklärt die genannten Prozesse auf einer höheren Ebene und zeigt, wie sie in PyTorch umgesetzt und kombiniert werden, um ein konvolutionales neuronales Netzwerk für eine Klassifizierungsaufgabe zu trainieren.
Voraussetzungen
- Bereite den Datensatz vor und verarbeite ihn (z. B. Normalisierung, Größenänderung).
- Nutze DataLoader für Batching und Shuffle-Training sowie Validierungsdaten.
- Definiere ein neuronales Netzwerkmodell mit
torch.nn.Module. - Wähle eine passende Verlustfunktion (z. B.
nn.CrossEntropyLossfür Klassifizierungen). - Wähle einen Optimierer (z. B. Adam, SGD).
- Implementiere Schleifen, um Modellgewichte zu aktualisieren, Verluste zu berechnen und Lernraten anzupassen.
- Bewerte die Modellleistung mit einer Validierungsschleife.
- Berechne die Genauigkeit mit
torch.maxfür Klassifizierungsaufgaben.
Importe und Setup
Nachfolgend sind einige der Bibliotheken aufgeführt, die für diese Aufgabe benötigt werden. Gradient Notebook’s Deep-Learning-Laufzeiten enthalten sie vorinstalliert.
import torch
import torch.nn as nn
import torch.nn.functional as F
import torchvision
import torchvision.transforms as transforms
import torchvision.datasets as Datasets
from torch.utils.data import Dataset, DataLoader
import numpy as np
import matplotlib.pyplot as plt
import cv2
from tqdm.notebook import tqdm
if torch.cuda.is_available():
device = torch.device('cuda:0')
print('Running on the GPU')
else:
device = torch.device('cpu')
print('Running on the CPU')
Anatomie Neural Networks
Neuronale Netzwerke bestehen aus Zahlen: Gewichten und Verzerrungen, die als Parameter bezeichnet werden. Ein Netzwerk mit 20 Millionen Parametern enthält 20 Millionen Zahlen, die jede Dateninstanz beeinflussen. Beispielsweise werden bei einem 28 x 28 Pixel großen Bild alle 784 Pixel von den 20 Millionen Parametern transformiert.
Modellziel
Das unten definierte ConvNet hat eine Ausgabeschicht, die einen zweielementigen Vektor erzeugt. Ziel des Modells ist es, eine binäre Klassifizierungsaufgabe zu lösen.
class ConvNet(nn.Module):
def __init__(self):
super().__init__()
self.conv1 = nn.Conv2d(3, 8, 3, padding=1)
self.batchnorm1 = nn.BatchNorm2d(8)
self.conv2 = nn.Conv2d(8, 8, 3, padding=1)
self.batchnorm2 = nn.BatchNorm2d(8)
self.pool2 = nn.MaxPool2d(2)
self.conv3 = nn.Conv2d(8, 32, 3, padding=1)
self.batchnorm3 = nn.BatchNorm2d(32)
self.conv4 = nn.Conv2d(32, 32, 3, padding=1)
self.batchnorm4 = nn.BatchNorm2d(32)
self.pool4 = nn.MaxPool2d(2)
self.conv5 = nn.Conv2d(32, 128, 3, padding=1)
self.batchnorm5 = nn.BatchNorm2d(128)
self.conv6 = nn.Conv2d(128, 128, 3, padding=1)
self.batchnorm6 = nn.BatchNorm2d(128)
self.pool6 = nn.MaxPool2d(2)
self.conv7 = nn.Conv2d(128, 2, 1)
self.pool7 = nn.AvgPool2d(3)
def forward(self, x):
#-------------
# INPUT
#-------------
x = x.view(-1, 3, 32, 32)
#-------------
# LAYER 1
#-------------
output_1 = self.conv1(x)
output_1 = F.relu(output_1)
output_1 = self.batchnorm1(output_1)
#-------------
# LAYER 2
#-------------
output_2 = self.conv2(output_1)
output_2 = F.relu(output_2)
output_2 = self.pool2(output_2)
output_2 = self.batchnorm2(output_2)
#-------------
# LAYER 3
#-------------
output_3 = self.conv3(output_2)
output_3 = F.relu(output_3)
output_3 = self.batchnorm3(output_3)
#-------------
# LAYER 4
#-------------
output_4 = self.conv4(output_3)
output_4 = F.relu(output_4)
output_4 = self.pool4(output_4)
output_4 = self.batchnorm4(output_4)
#-------------
# LAYER 5
#-------------
output_5 = self.conv5(output_4)
output_5 = F.relu(output_5)
output_5 = self.batchnorm5(output_5)
#-------------
# LAYER 6
#-------------
output_6 = self.conv6(output_5)
output_6 = F.relu(output_6)
output_6 = self.pool6(output_6)
output_6 = self.batchnorm6(output_6)
#--------------
# OUTPUT LAYER
#--------------
output_7 = self.conv7(output_6)
output_7 = self.pool7(output_7)
output_7 = output_7.view(-1, 2)
return F.softmax(output_7, dim=1)
Das richtige Training
Trainiere das Modell, indem du Daten in Batches aufteilst, den Verlust berechnest (Forward Propagation) und die Parameter anpasst (Backpropagation). Wiederhole diesen Vorgang für alle Batches, bis das Training abgeschlossen ist.
def train(network, training_set, batch_size, optimizer, loss_function):
"""
This function optimizes the convnet weights
"""
# creating list to hold loss per batch
loss_per_batch = []
# defining dataloader
train_loader = DataLoader(training_set, batch_size)
# iterating through batches
print('training...')
for images, labels in tqdm(train_loader):
#---------------------------
# sending images to device
#---------------------------
images, labels = images.to(device), labels.to(device)
#-----------------------------
# zeroing optimizer gradients
#-----------------------------
optimizer.zero_grad()
#-----------------------
# classifying instances
#-----------------------
classifications = network(images)
#---------------------------------------------------
# computing loss/how wrong our classifications are
#---------------------------------------------------
loss = loss_function(classifications, labels)
loss_per_batch.append(loss.item())
#------------------------------------------------------------
# computing gradients/the direction that fits our objective
#------------------------------------------------------------
loss.backward()
#---------------------------------------------------
# optimizing weights/slightly adjusting parameters
#---------------------------------------------------
optimizer.step()
print('all done!')
return loss_per_batch
[/dm_code_snippet>
Generalisierung und Validierung
Testen Sie die optimierten Parameter auf einem separaten Validierungsdatensatz, um sicherzustellen, dass sie auf neue Daten generalisiert werden können. Während der Validierung erfolgt keine weitere Optimierung der Parameter.
def validate(network, validation_set, batch_size, loss_function):
"""
This function validates convnet parameter optimizations
"""
# creating a list to hold loss per batch
loss_per_batch = []
# defining model state
network.eval()
# defining dataloader
val_loader = DataLoader(validation_set, batch_size)
print('validating...')
# preventing gradient calculations since we will not be optimizing
with torch.no_grad():
# iterating through batches
for images, labels in tqdm(val_loader):
#--------------------------------------
# sending images and labels to device
#--------------------------------------
images, labels = images.to(device), labels.to(device)
#--------------------------
# making classsifications
#--------------------------
classifications = network(images)
#-----------------
# computing loss
#-----------------
loss = loss_function(classifications, labels)
loss_per_batch.append(loss.item())
print('all done!')
return loss_per_batch
Leistungsmessung
Vergleichen Sie die Vorhersagen des Modells mit den tatsächlichen Labels, um die Genauigkeit zu berechnen. Dies gilt insbesondere bei Klassifizierungsaufgaben mit ausgewogenen Datensätzen.
def accuracy(network, dataset):
"""
This function computes accuracy
"""
# setting model state
network.eval()
# instantiating counters
total_correct = 0
total_instances = 0
# creating dataloader
dataloader = DataLoader(dataset, 64)
# iterating through batches
with torch.no_grad():
for images, labels in tqdm(dataloader):
images, labels = images.to(device), labels.to(device)
#-------------------------------------------------------------------------
# making classifications and deriving indices of maximum value via argmax
#-------------------------------------------------------------------------
classifications = torch.argmax(network(images), dim=1)
#--------------------------------------------------
# comparing indicies of maximum values and labels
#--------------------------------------------------
correct_predictions = sum(classifications==labels).item()
#------------------------
# incrementing counters
#------------------------
total_correct+=correct_predictions
total_instances+=len(images)
return round(total_correct/total_instances, 3)
Datensatz
Verwenden Sie den CIFAR-10-Datensatz, um die Prozesse in der Praxis zu demonstrieren. Der Datensatz enthält Bilder mit einer Auflösung von 32 x 32 Pixeln, die in 10 Klassen unterteilt sind.
# Laden der Trainingsdaten
training_set = Datasets.CIFAR10(root='./', download=True,
transform=transforms.ToTensor())
# Laden der Validierungsdaten
validation_set = Datasets.CIFAR10(root='./', download=True, train=False,
transform=transforms.ToTensor())
Architektur des ConvNet
Passen Sie das ConvNet an, um einen Vektor mit 10 Elementen auszugeben, da es sich um eine Klassifizierungsaufgabe mit 10 Klassen handelt. Hier ist der Code:
class ConvNet(nn.Module):
def __init__(self):
super().__init__()
self.conv1 = nn.Conv2d(3, 8, 3, padding=1)
self.batchnorm1 = nn.BatchNorm2d(8)
self.conv2 = nn.Conv2d(8, 8, 3, padding=1)
self.batchnorm2 = nn.BatchNorm2d(8)
self.pool2 = nn.MaxPool2d(2)
self.conv3 = nn.Conv2d(8, 32, 3, padding=1)
self.batchnorm3 = nn.BatchNorm2d(32)
self.conv4 = nn.Conv2d(32, 32, 3, padding=1)
self.batchnorm4 = nn.BatchNorm2d(32)
self.pool4 = nn.MaxPool2d(2)
self.conv5 = nn.Conv2d(32, 128, 3, padding=1)
self.batchnorm5 = nn.BatchNorm2d(128)
self.conv6 = nn.Conv2d(128, 128, 3, padding=1)
self.batchnorm6 = nn.BatchNorm2d(128)
self.pool6 = nn.MaxPool2d(2)
self.conv7 = nn.Conv2d(128, 10, 1)
self.pool7 = nn.AvgPool2d(3)
def forward(self, x):
#-------------
# INPUT
#-------------
x = x.view(-1, 3, 32, 32)
#-------------
# LAYER 1
#-------------
output_1 = self.conv1(x)
output_1 = F.relu(output_1)
output_1 = self.batchnorm1(output_1)
#-------------
# LAYER 2
#-------------
output_2 = self.conv2(output_1)
output_2 = F.relu(output_2)
output_2 = self.pool2(output_2)
output_2 = self.batchnorm2(output_2)
#-------------
# LAYER 3
#-------------
output_3 = self.conv3(output_2)
output_3 = F.relu(output_3)
output_3 = self.batchnorm3(output_3)
#-------------
# LAYER 4
#-------------
output_4 = self.conv4(output_3)
output_4 = F.relu(output_4)
output_4 = self.pool4(output_4)
output_4 = self.batchnorm4(output_4)
#-------------
# LAYER 5
#-------------
output_5 = self.conv5(output_4)
output_5 = F.relu(output_5)
output_5 = self.batchnorm5(output_5)
#-------------
# LAYER 6
#-------------
output_6 = self.conv6(output_5)
output_6 = F.relu(output_6)
output_6 = self.pool6(output_6)
output_6 = self.batchnorm6(output_6)
#--------------
# OUTPUT LAYER
#--------------
output_7 = self.conv7(output_6)
output_7 = self.pool7(output_7)
output_7 = output_7.view(-1, 10)
return F.softmax(output_7, dim=1)
Zusammenführung der Prozesse
Kombinieren Sie das Training und die Validierung in einer Funktion oder Klasse, um den gesamten Prozess zu optimieren und synchron zu halten.
# Instanziieren des Modells
model = ConvNet()
# Definieren des Optimierers
optimizer = torch.optim.Adam(model.parameters(), lr=3e-4)
# Training
training_losses = train(network=model, training_set=training_set,
batch_size=64, optimizer=optimizer,
loss_function=nn.CrossEntropyLoss())
# Validierung
validation_losses = validate(network=model, validation_set=validation_set,
batch_size=64, loss_function=nn.CrossEntropyLoss())
# Genauigkeit berechnen
training_accuracy = accuracy(model, training_set)
print(f'Training Accuracy: {training_accuracy}')
validation_accuracy = accuracy(model, validation_set)
print(f'Validation Accuracy: {validation_accuracy}')
Optimales Training für Convolutional Neural Networks
Beim Training eines neuronalen Netzes kann es vorkommen, dass die Genauigkeit zunächst suboptimal ist. Eine effektive Technik zur Leistungssteigerung besteht darin, die ersten vier Codezeilen in eine neue Code-Zelle zu verschieben und das Training erneut auszuführen. Dieser Prozess, bei dem das gesamte Dataset mehrfach durchlaufen wird, wird als Training für mehrere Epochen bezeichnet. Trainierst du dein Modell fünfmal, dann bedeutet das, dass es für fünf Epochen trainiert wurde.
Warum ist das Verschieben der Codezeilen wichtig?
Wenn du das Training startest, werden die Gewichte des Modells zufällig initialisiert und dann optimiert. Wenn du jedoch die Modell-Initialisierung erneut in derselben Code-Zelle ausführst, werden die Gewichte wieder zufällig gesetzt, wodurch die vorherige Optimierung verloren geht. Um dies zu vermeiden, solltest du alle Prozesse sauber in einer Funktion oder einer Klasse kapseln. Eine besonders elegante Lösung bietet eine Python-Klasse, da sie alle Prozesse in einer strukturierten Form zusammenfasst.
Implementierung eines Convolutional Neural Networks
class ConvolutionalNeuralNet():
def __init__(self, network):
self.network = network.to(device)
self.optimizer = torch.optim.Adam(self.network.parameters(), lr=1e-3)
def train(self, loss_function, epochs, batch_size, training_set, validation_set):
log_dict = {
'training_loss_per_batch': [],
'validation_loss_per_batch': [],
'training_accuracy_per_epoch': [],
'validation_accuracy_per_epoch': []
}
def init_weights(module):
if isinstance(module, nn.Conv2d):
torch.nn.init.xavier_uniform_(module.weight)
module.bias.data.fill_(0.01)
elif isinstance(module, nn.Linear):
torch.nn.init.xavier_uniform_(module.weight)
module.bias.data.fill_(0.01)
def accuracy(network, dataloader):
network.eval()
total_correct = 0
total_instances = 0
for images, labels in tqdm(dataloader):
images, labels = images.to(device), labels.to(device)
predictions = torch.argmax(network(images), dim=1)
total_correct += sum(predictions == labels).item()
total_instances += len(images)
return round(total_correct / total_instances, 3)
self.network.apply(init_weights)
train_loader = DataLoader(training_set, batch_size)
val_loader = DataLoader(validation_set, batch_size)
self.network.train()
for epoch in range(epochs):
print(f'Epoch {epoch + 1}/{epochs}')
train_losses = []
print('Training...')
for images, labels in tqdm(train_loader):
images, labels = images.to(device), labels.to(device)
self.optimizer.zero_grad()
predictions = self.network(images)
loss = loss_function(predictions, labels)
log_dict['training_loss_per_batch'].append(loss.item())
train_losses.append(loss.item())
loss.backward()
self.optimizer.step()
with torch.no_grad():
print('Berechnung der Trainingsgenauigkeit...')
train_accuracy = accuracy(self.network, train_loader)
log_dict['training_accuracy_per_epoch'].append(train_accuracy)
print('Validierung...')
val_losses = []
self.network.eval()
with torch.no_grad():
for images, labels in tqdm(val_loader):
images, labels = images.to(device), labels.to(device)
predictions = self.network(images)
val_loss = loss_function(predictions, labels)
log_dict['validation_loss_per_batch'].append(val_loss.item())
val_losses.append(val_loss.item())
print('Berechnung der Validierungsgenauigkeit...')
val_accuracy = accuracy(self.network, val_loader)
log_dict['validation_accuracy_per_epoch'].append(val_accuracy)
train_losses = np.array(train_losses).mean()
val_losses = np.array(val_losses).mean()
print(f'training_loss: {round(train_losses, 4)} training_accuracy: ' +
f'{train_accuracy} validation_loss: {round(val_losses, 4)} ' +
f'validation_accuracy: {val_accuracy}\n')
return log_dict
def predict(self, x):
return self.network(x)
Warum diese Architektur?
In der obigen Klasse werden Training und Validierung in der Methode train() kombiniert, um mehrere Aufrufe zu vermeiden, da beide Prozesse zusammenhängen. Die Genauigkeit wird nach jeder Trainings- und Validierungsschleife berechnet, um den Fortschritt zu verfolgen. Zudem ist eine Gewichtsinitialisierungsfunktion enthalten, die Xavier Weight Initialization verwendet – eine bewährte Methode, um eine gute Startkonfiguration für das Training sicherzustellen.
Modelltraining mit 10 Epochen
model = ConvolutionalNeuralNet(ConvNet())
log_dict = model.train(nn.CrossEntropyLoss(), epochs=10, batch_size=64,
training_set=training_set, validation_set=validation_set)
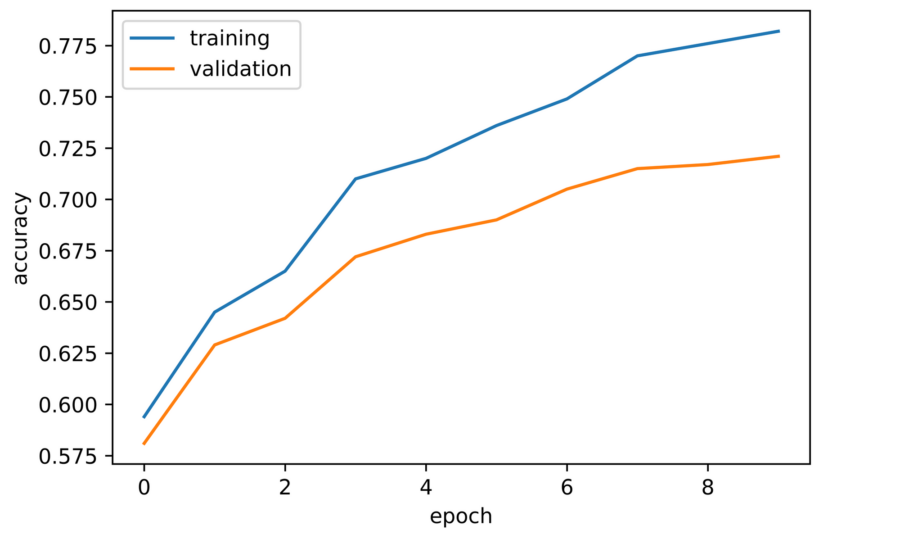
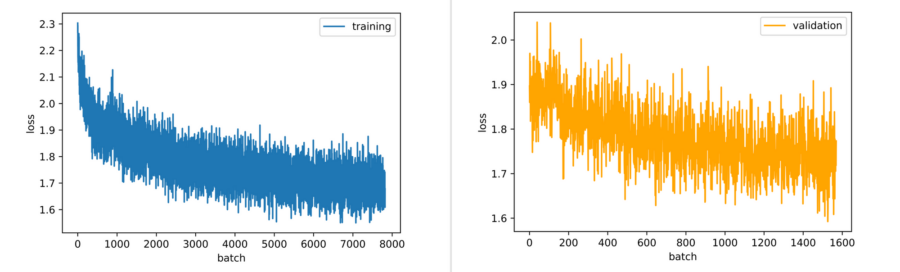
Nach dem Training des Convolutional Neural Networks für 10 Epochen ergaben sich die folgenden Ergebnisse:
-
- Die Trainingsgenauigkeit und Validierungsgenauigkeit stiegen während des Trainings.
- Die Validierungsgenauigkeit begann bei ca. 58 % und erreichte 72 % in der zehnten Epoche.
- Die Verlustkurve zeigte einen stetigen Rückgang, was darauf hindeutet, dass das Modell weiterhin lernen kann.
Abschlussbemerkungen zu Deep Learning mit PyTorch
Dieses Tutorial zeigt, wie Sie Trainings-, Validierungs- und Genauigkeitsprozesse in PyTorch implementieren. Die Schritte wurden in eine effiziente und wiederverwendbare Struktur integriert, die sich für reale Projekte anwenden lässt.