Das Rucksackproblem: Eine Lösung mit C++

In diesem Artikel lernen wir, das Rucksackproblem mit C++ zu lösen. Wir beginnen mit der Problemstellung und gehen dann zur Lösung über. Dieses Problem gehört zu den vielen bekannten klassischen Problemen. Es unterscheidet sich erheblich von seinen Geschwistern, dem 0-1-Rucksack und dem 0-N-Rucksack. Es handelt sich um einen gierigen Algorithmus, während die anderen beiden dynamische Programmieralgorithmen sind.

Was ist das Rucksackproblem?

Sie haben eine Liste mit Gewichten und Preisen bestimmter Gegenstände sowie einen Rucksack mit einer bestimmten Kapazität, sagen wir W. Ihre Aufgabe besteht darin, diesen Rucksack so zu füllen, dass der Gesamtpreis aller in den Rucksack aufgenommenen Gegenstände für alle Konfigurationen maximal ist. Sie können jeden Gegenstand entweder vollständig oder als Bruchteil aufnehmen.

Rucksack-Algorithmus

Schauen wir uns den Algorithmus zur Lösung dieses Problems an. Da wir eine gierige Lösung für dieses Problem implementieren werden, folgt hier eine kurze Beschreibung gieriger Algorithmen.

Was ist ein gieriger Algorithmus?

Bei diesen Algorithmen versuchen wir, bei jedem Schritt ein lokales Maximum/Minimum zu erreichen, um am Ende ein globales Maximum/Minimum zu erzielen. Das bedeutet, dass wir die Antwort auf jedes Teilproblem maximieren/minimieren und so zur maximalen/minimalen Antwort des Gesamtproblems gelangen.

Hinweis: Die gierige Wahl, die Sie treffen, muss ein sicherer Schritt sein.

Sicherer Schritt: Ein Schritt wird als sicher bezeichnet, wenn es eine optimale Antwort gibt, die mit diesem Anfangsschritt übereinstimmt.

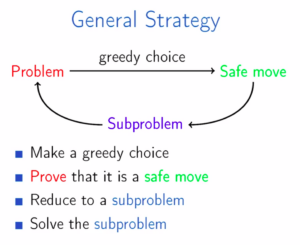
Strategie zur Arbeit mit gierigen Algorithmen

Nachfolgend sind die Schritte aufgeführt, die Sie befolgen sollten, um einen perfekten gierigen Algorithmus zu entwickeln.

• Treffen Sie eine gierige Wahl
• Beweisen Sie, dass es ein sicherer Schritt ist, damit Sie nicht den Code schreiben und am Ende feststellen, dass es keine machbare Wahl war. Dieser spezielle Schritt ist der wichtigste Schritt gieriger Algorithmen.
• Reduzieren Sie das Problem auf ein kleineres Problem
• Lösen Sie alle kleineren Probleme.

Pseudocode

Nun gehen wir den Rucksack-Algorithmus Schritt für Schritt durch.

1. Sortieren Sie die Gegenstände in absteigender Reihenfolge nach dem Wert-/Gewichtsverhältnis. Dieser Schritt allein verringert die Zeitkomplexität der Auswahl des besten Gegenstands von O(N) auf O(log2N).
2. Nun beginnen wir mit der Auswahl der Objekte, indem wir eine for-Schleife von i = 0 bis i = N durchlaufen.
3. Lemma: Es gibt eine optimale Lösung, die so viel wie möglich von einem Gegenstand mit dem maximalen Wert pro Gewichtseinheit verwendet.
4. Beweis: Versuchen Sie, den Rucksack nach anderen Auswahlkriterien zu füllen, Sie erhalten immer einen kleineren Gesamtwert als den maximal möglichen Wert. Das unten angehängte Beispiel beweist, dass unser Lemma korrekt ist.

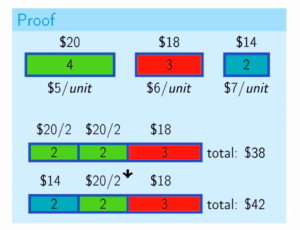
Wenn die Größe des Gegenstands mit dem maximalen Wert-/Gewichtsverhältnis in den Rucksack passt, nehmen Sie den gesamten Gegenstand. Andernfalls nehmen Sie den maximal möglichen Bruchteil davon.

• Reduzieren Sie die Kapazität des Rucksacks um das Gewicht des aufgenommenen Gegenstands.
• Wenn der gesamte Gegenstand aufgenommen wird: Kapazität = Kapazität – Gewicht[dieser_Gegenstand].
• Andernfalls wird die Kapazität 0, da der Rucksack voll wird.
• Fügen Sie den Wert des aufgenommenen Bruchteils dieses Gegenstands zum Gesamtwert hinzu.
• Wenn der gesamte Gegenstand aufgenommen wird: Gesamtwert += Wert[dieser_Gegenstand]
• Andernfalls: Wert += Bruchteil_des_aufgenommenen_Gewichts * Wert[dieser_Gegenstand].
• Wenn die Kapazität 0 wird, beenden Sie die Schleife.

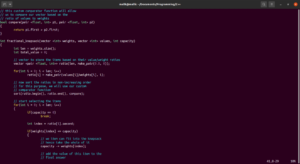
Die Gesamtstruktur des Pseudocodes wird:

Rucksackproblem: C++-Programm zur Demonstration

#include <iostream>
#include <algorithm>
#include <vector>

using namespace std;

// Diese benutzerdefinierte Vergleichsfunktion ermöglicht es uns,
// unseren Vektor basierend auf dem Verhältnis von Werten zu Gewichten zu vergleichen
bool compare(pair <float, int> p1, pair <float, int> p2)
{
	return p1.first > p2.first;
}

int fractional_knapsack(vector <int> weights, vector <int> values, int capacity)
{
	int len = weights.size();
	int total_value = 0;

	// Vektor zum Speichern der Elemente basierend auf ihren Wert-/Gewichtsverhältnissen
	vector <pair <float, int>> ratio(len, make_pair(0.0, 0));

	for(int i = 0; i < len; i++)
		ratio[i] = make_pair(values[i]/weights[i], i);

	// Sortieren Sie die Verhältnisse in nicht aufsteigender Reihenfolge
	// Zu diesem Zweck verwenden wir unsere benutzerdefinierte Vergleichsfunktion
	sort(ratio.begin(), ratio.end(), compare);

	// Beginnen Sie mit der Auswahl der Gegenstände
	for(int i = 0; i < len; i++)
	{
		if(capacity == 0)
			break;

		int index = ratio[i].second;

		if(weights[index] <= capacity)
		{
			// Dieser Gegenstand passt in den Rucksack,
			// daher nehmen wir den gesamten Gegenstand
			capacity -= weights[index];

			// Fügen Sie den Wert dieses Gegenstands zur endgültigen Antwort hinzu
			total_value += values[index];
		}
		else
		{
			// Dieser Gegenstand passt nicht in den Rucksack
			// und daher nehmen wir einen Bruchteil davon
			int value_to_consider = values[index] * (float(capacity)/float(weights[index]));
			total_value += value_to_consider;
			capacity = 0;
		}
	}

	return total_value;
}

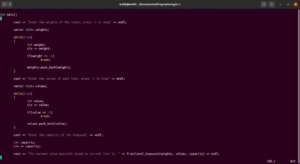
int main()
{
	cout << "Geben Sie die Gewichte der Gegenstände ein, drücken Sie -1 zum Beenden" << endl;

	vector <int> weights;

	while(true)
	{
		int weight;
		cin >> weight;

		if(weight == -1)
			break;

		weights.push_back(weight);
	}

	cout << "Geben Sie die Werte jedes Gegenstands ein, drücken Sie -1 zum Beenden" << endl;
	
	vector <int> values;

	while(true)
	{
		int value;
		cin >> value;

		if(value == -1)
			break;

		values.push_back(value);
	}

	cout << "Geben Sie die Kapazität des Rucksacks ein" << endl;

	int capacity;
	cin >> capacity;

	cout << "Der maximal mögliche Wert basierend auf der aktuellen Liste ist: " << fractional_knapsack(weights, values, capacity) << endl;
}

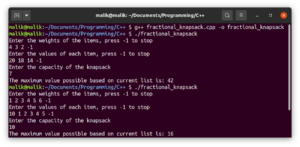
Ausgabe

Fazit

Der Rucksack ist ein gieriger Algorithmus, und in diesem Artikel haben wir uns seine Implementierung angesehen. Wir haben kurz über die gierigen Algorithmen gesprochen, dann den Pseudocode des Rucksack-Algorithmus diskutiert. Wir haben bewiesen, dass unsere gierige Wahl ein sicherer Schritt ist, und am Ende haben wir ein C++-Programm geschrieben, um diese Lösung zu demonstrieren. Die Gesamtlaufzeitkomplexität dieses Konzepts beträgt: O(Nlog2N). Das war es für heute, danke fürs Lesen.

Weiterführende Literatur

Wenn Sie mehr über Rucksack- und andere gierige Algorithmen erfahren möchten, können Sie die folgenden Websites besuchen.

https://brilliant.org/wiki/greedy-algorithm

https://en.wikipedia.org/wiki/Knapsack_problem