Binärbäume: Höhe rekursiv und iterativ berechnen

Binärbäume

Binärbäume sind eine Datenstruktur, in der Daten hierarchisch und nicht linear (wie in LinkedLists und Arrays) gespeichert werden. Eine Binärbaum-Datenstruktur besteht aus Knoten. Jeder Knoten enthält die Daten zusammen mit den Referenzen zu den Kinderzeigern (links und rechts). Die Wurzel des Binärbaums ist der oberste Knoten (also das Gegenteil eines tatsächlichen Baumes). Die folgende Abbildung zeigt einen Baum mit einigen Knoten.

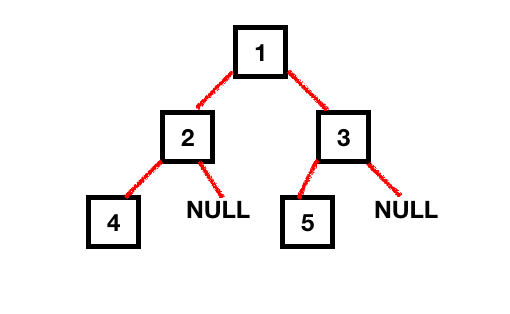Die Höhe eines Knotens ist die Länge des längsten Weges nach unten zu einem Blatt von diesem Knoten. Die Höhe der Wurzel ist die Höhe des Baumes. Um die Höhe des Baumes zu berechnen, müssen wir jeden Knoten des Baumes durchlaufen, um alle Permutationen und Kombinationen zu erhalten. Es gibt zwei Möglichkeiten, die Höhe des Baumes zu berechnen.

• Rekursiver Weg
• Iterativer Weg

Höhe eines Baumes – Rekursiv

Die Rekursion beinhaltet die Berechnung der Ergebnisse der Teilprobleme und die Rückgabe an das übergeordnete Problem.

Schritte:

1. Um die Höhe des Baumes rekursiv zu berechnen, müssen wir die Höhe seines linken Teilbaums und rechten Teilbaums rekursiv finden und 1 hinzufügen (Höhe zwischen dem obersten Knoten und seinen Kindern).
2. Jeder dieser Teilbäume könnte selbst einen linken und rechten Teilbaum haben, daher würde die Rekursion gelten, bis die Teilbäume NULL sind. Die Höhe eines Nullbaumknotens ist -1.
3. Schließlich vergleichen wir die Höhen des linken und rechten Teilbaums und geben die größere zurück.

Die folgende Abbildung zeigt die Anzahl der Permutationen zur Berechnung der Höhe des Binärbaums.

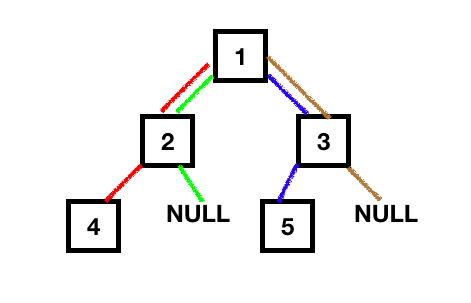Lassen Sie uns das Java-Programm schreiben, um die Höhe des Baumes rekursiv zu berechnen. Zuerst haben wir eine grundlegende Implementierung der Baum-Datenstruktur.

package com.journaldev.tree.height;

public class BinaryTree {

	TreeNode root;

	public static class TreeNode {

		TreeNode left;
		TreeNode right;
		Object data;

		TreeNode(Object data) {
			this.data = data;
			left = right = null;
		}
	}
}

Lassen Sie uns den Code zum Finden der Baumhöhe mithilfe von Rekursion sehen.

package com.journaldev.tree.height;

import com.journaldev.tree.height.BinaryTree.TreeNode;

public class HeightOfTree {

	public static void main(String[] args) {

		BinaryTree binaryTree = new BinaryTree();

		/**
		 * Binärbaum in unserem Beispiel, Höhe = 2
		 * 		1		(Wurzel)
		 * 	  2	  3		(Ebene 1)
		 *  4    	 5		(Ebene 2)
		 */
		binaryTree.root = new TreeNode(1);
		binaryTree.root.left = new TreeNode(2);
		binaryTree.root.right = new TreeNode(3);
		binaryTree.root.left.left = new TreeNode(4);
		binaryTree.root.right.left = new TreeNode(5);

		int heightOfTree = height(binaryTree.root);
		System.out.printf("Höhe des Baumes ist %d", heightOfTree);
	}
	
	public static int height(TreeNode root) {

		if (root == null)
			return -1;

		int leftHeight = height(root.left);
		int rightHeight = height(root.right);

		return Math.max(leftHeight, rightHeight) + 1;
	}
}

Im obigen Code fügen wir, sobald wir den untersten Kindknoten erreicht haben, eins zur Höhe des Baumes hinzu und geben das Ergebnis an den vorherigen Aufruf zurück.

Ausgabe: Höhe des Baumes ist 2

Nun berechnen wir dasselbe nicht-rekursiv.

Höhe des Baumes – Iterativ

Um die Höhe des Baumes iterativ zu berechnen, müssen wir einfach die Anzahl der Ebenen im Baum berechnen.

Schritte:

1. Erstellen Sie eine Queue und fügen Sie die Wurzel des Baumes hinzu.
2. Entfernen Sie den Knoten aus der Queue und durchlaufen Sie die Queue, während Sie die Kinderknoten zur Queue hinzufügen.
3. In jeder Iteration entfernen Sie das zuletzt hinzugefügte Element aus der Queue und fügen die Elemente der nächsten Ebene (dieses Elements) zur Queue hinzu.
4. Machen Sie dies, bis die Queuegröße null wird. Das würde bedeuten, dass die nächste Ebene null Elemente hat.
5. Für jede durchlaufene Ebene addieren Sie 1.

Folgendes ist das iterative Programm zur Berechnung der Baumhöhe.

public static int heightIteratively(TreeNode root) {

    if (root == null)
        return -1;

    Queue queue = new LinkedList<>();
    queue.add(root);
    int height = -1;

    while (!queue.isEmpty()) {
        int size = queue.size();

        height++;

        while (size > 0) {
            TreeNode treeNode = queue.remove();

            if (treeNode.left != null)
                queue.add(treeNode.left);

            if (treeNode.right != null)
                queue.add(treeNode.right);
            
            size--;
        }
    }
    return height;
}

Der obige Code läuft weiter, bis die Queue leer ist. Außerdem werden alle Elemente der nächsten Ebene hinzugefügt, während die aktuellen Ebenenelemente aus der Queue entfernt werden.

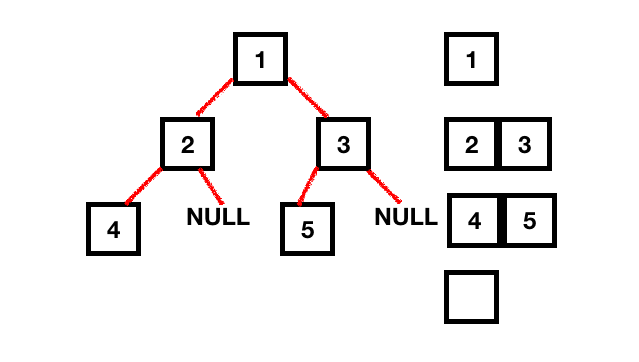Die Zeitkomplexität beträgt O(n). Die Platzkomplexität beträgt O(1).

Fazit

Zusammenfassend lässt sich sagen, dass das Verständnis von Binärbäumen: Höhe rekursiv & iterativ berechnen wesentlich ist, um Baumdatenstrukturen zu meistern. Durch die Untersuchung sowohl rekursiver als auch iterativer Ansätze können Sie die Baumhöhe effizient bestimmen und dabei tiefere Einblicke in die Algorithmusgestaltung und -implementierung gewinnen. Egal, ob Sie komplexe Probleme lösen oder skalierbare Anwendungen erstellen, diese Methoden bieten die Grundlage für effektive Baummanipulationen in der Programmierung.